9.2 Taking Fairness Seriously

Recall the steps for prediction/classification

  1. Choose Approach
    • We will use a regression to try to classify subjects as those who will / will not recidivate
  2. Check accuracy
    • We will calculate false positive rates and false negative rates
    • We will use cross-validation to do so
    • What about fairness?
  3. Iterate

The performance of a prediction/classification may be different for different groups in the population. Dressel and Farid point to this when it comes to different racial groups.

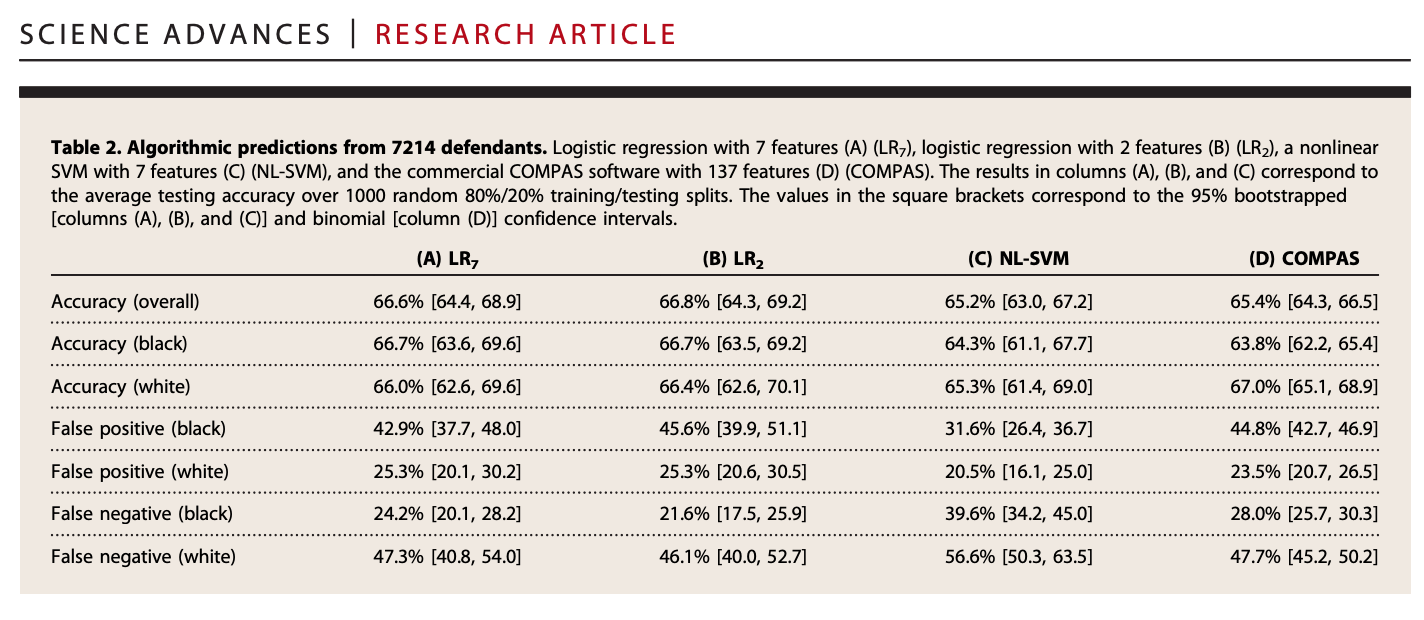
Dressel and Farid

Let’s see how our predictions perform across racial groups

race: 1: White (Caucasian); 2: Black (African American); 3: Hispanic; 4: Asian; 5: Native American; 6: Other

Wait a second– we didn’t use race in our model. Why could the performance still differ across racial groups?

  • Think about how the inputs in our regression model could be correlated with race.
  • Think about how existing human biases and inequalities that lead to differential arrest rates by racial groups could be reproduced in our model.
  • Even if a model does not have the intent to include race, its impact may nonetheless vary according to race. This could be true for any number of characteristics depending on the application.

We will subset our data by race.

black <- subset(broward, race == 2)
white <- subset(broward, race == 1)

We can first check overall accuracy

mean(black$cvpredictions == black$two_year_recid)
## [1] 0.6696429
mean(white$cvpredictions == white$two_year_recid)
## [1] 0.6805216

But are we making the same types of errors?

## False positive rate- Black
## Out of those who do not recidivate, how often did we predict recidivate?
fprate.black <- sum(black$cvpredictions == 1 & black$two_year_recid == 0) / 
  sum(black$two_year_recid == 0)

## False negative rate- Black
## Out of those who recidivate, how often does it predict not recidivate?
fnrate.black <-sum(black$cvpredictions== 0 & black$two_year_recid == 1) / 
  sum(black$two_year_recid == 1)

## False positive rate- white
fprate.white <- sum(white$cvpredictions == 1 & white$two_year_recid == 0) / 
  sum(white$two_year_recid == 0)

## False negative rate- white
fnrate.white <-sum(white$cvpredictions== 0 & white$two_year_recid == 1) / 
  sum(white$two_year_recid == 1)

Let’s see how our predictions perform across racial groups

## False positive rates
fprate.black
## [1] 0.2846797
fprate.white 
## [1] 0.1323925
## False negative rates
fnrate.black
## [1] 0.3734876
fnrate.white 
## [1] 0.6076605

We see asymmetries in the types of errors the model is making across racial groups. Black subjects have higher false positives– more likely as being predicted to recidivate (a predicted “positive”) when they do not (the “false” in false positive). White subjects have higher false negatives– predicted not to recidivate (the negative) when they do (the false in false negative).

Based on these results, reflect on the following:

  • Should we use this type of algorithm in public policy?
    • What might be desirable about this process over alternatives?
    • What are possible concerns?
    • Does your answer depend on accuracy or other considerations?
  • What should we care more about? False positives or false negatives?
  • What measures of fairness should be considered?
  • Are there ways to avoid an unfair/biased model?

9.2.1 Extended Learning

Note: There are many debates about the use of these algorithms

  • Example of Initial Critique from ProPublica
  • Example of Rejoinder
  • Discussion of what fairness means: J. Kleinberg, S. Mullainathan, M. Raghavan, Inherent trade-offs in the fair determination of risk scores. (2016).
    • Notes that goals of fairness can be in competition:
    • Well-calibrated: if the algorithm identifies a set of people as having a probability z of constituting positive instances, then approximately a z fraction of this set should indeed be positive instances
    • Balance for positive and negative instances across groups: the chance of making a mistake on should not depend on which group they belong to.

For more on fairness and machine learning