Section 7 Quantities of Interest

This section will provide information about calculating quantities of interest. Often, in linear regression, our coefficients might directly represent the quantities we are interested in interpreting. However, in other models, we might need to do a bit of work to make it easier on our readers (and ourselves).

The quantities of interest you generate should be directly related to your research question and hypotheses. For example, if my hypothesis was about how the competitiveness of a state is related to the probability that someone is contacted by a campaign, then my quantities of interest would involve a comparison of the predicted probability of campaign contact for those in more vs. less competitive states. In contrast, if my hypothesis was about the number of bills passed in a legislature under unified vs. divided government, I would want to express my quantities of interest as a different in counts of bills or rate of bills pasesed.

We will discuss computing quantities of interest, uncertainty for these quantities, and visualization.

We can take something that looks like column 5 in the table from Antoine Banks and Heather Hicks example from the previous section and move it into a figure, as the authors did.

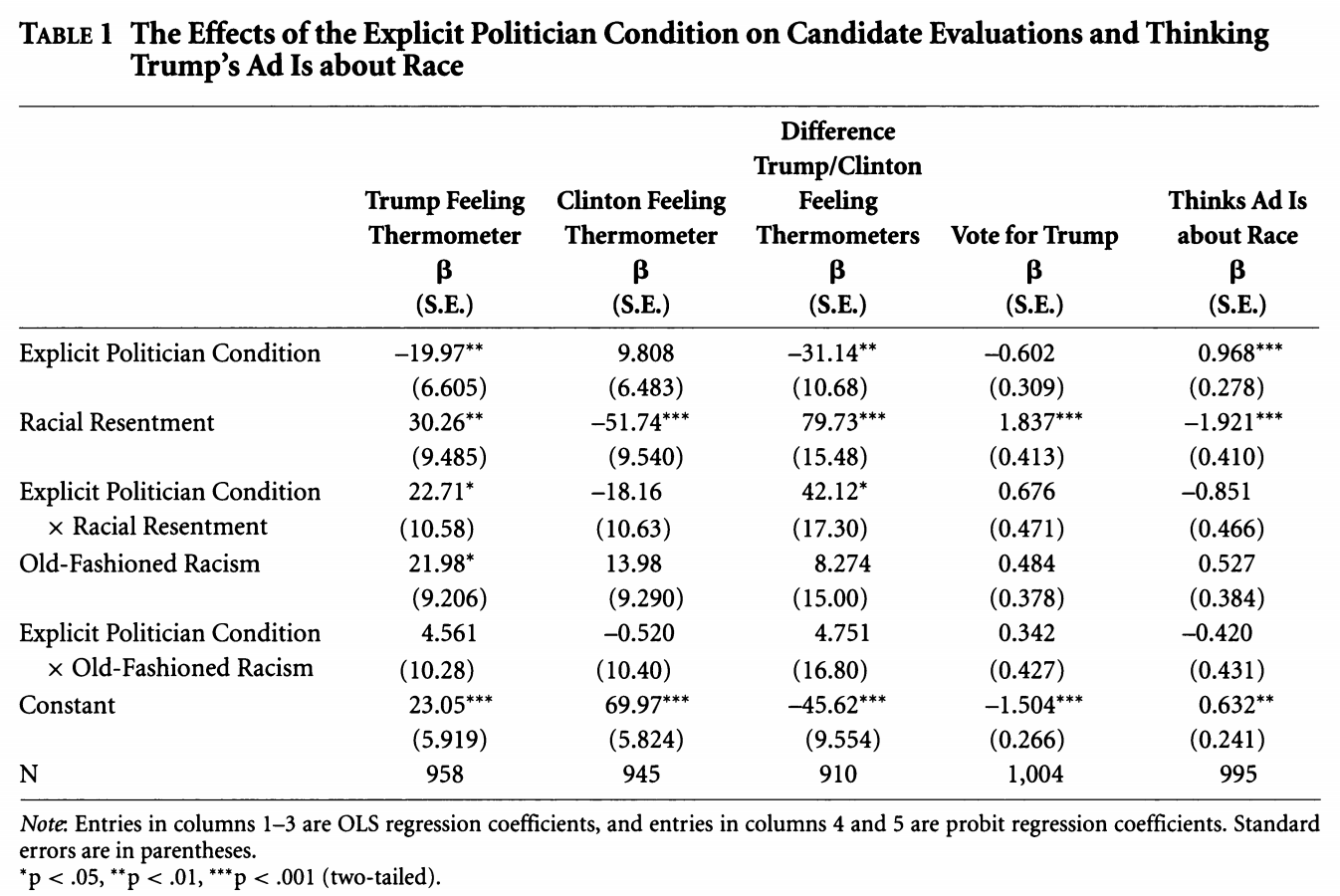
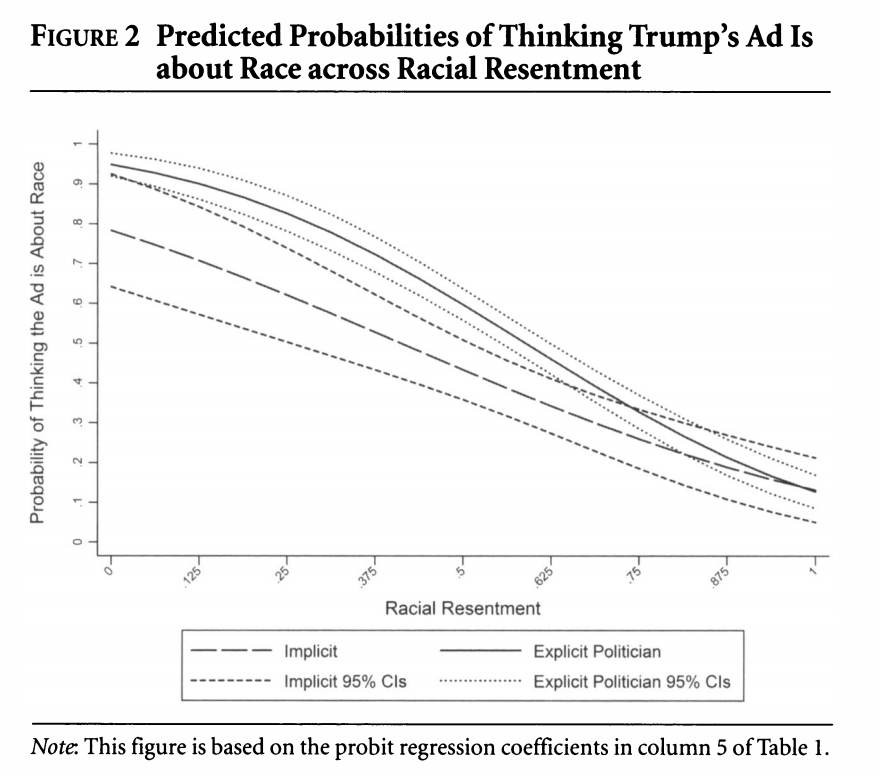
Here are a few external resources that relate to the concepts discussed in this section.